Reversing and solving nested puzzles | Picasso @ FCSC 2023
Intro
Yes, this is yet another puzzle reversing challenge from \J for the FCSC 2023,
yes I swear I’m also able to flag other types of challenges too, I can’t help I
like algorithms too much. I will try to make lower level content soon ™️
👀.
Yes I also know that face0xff already did a
writeup on this, but I still want
to writeup it because I liked the challenge and even though my solution is kind
of overengineered compared to the one of face0xff, I really enjoyed writing
the solver algorithm for the first puzzle so here you go.

Challenge description
reverse | 482 pts 8 solves ⭐⭐⭐
Trouvez une entrée permettant d'afficher le message de réussite, et envoyez-la
sur le service distant pour récupérer le flag.
nc challenges.france-cybersecurity-challenge.fr 2251
SHA256(picasso) =
f3d6aafce2c069fdf486fce75112ccc09593ddd54452407d4cf066be12daf7fd.
Author: \J
Given files
Writeup
Reverse
Overview
OK, nothing magic you know how this works: it’s a puzzle, we need to find the
input that solves said puzzle. Now the twist is that knowing how \J writes his
challenges, the problem is either NP-complete, obfuscated with 50+ nanomites or
put together with 12 other puzzles that must be solved together with the same
input. Make your bet, which one is it this time ?
So I open up my decompiler and I find a single function, the whole thing holds
in a single function in less than 0x200 bytes of machine code. Let’s look this
up.
char init_state[0x36] =
{
0x0d, 0x03, 0x02, 0x0e, 0x0f, 0x09, 0x07, 0x0e, 0x0d, 0x06, 0x03, 0x02, 0x07, 0x02, 0x08, 0x0e,
0x07, 0x04, 0x04, 0x03, 0x0d, 0x04, 0x0c, 0x03, 0x0f, 0x02, 0x0a, 0x05, 0x09, 0x01, 0x06, 0x0a,
0x0b, 0x02, 0x05, 0x0c, 0x0e, 0x0b, 0x0d, 0x01, 0x0a, 0x01, 0x05, 0x09, 0x01, 0x0f, 0x06, 0x0e,
0x04, 0x04, 0x0b, 0x04, 0x0b, 0x0f, 0x00
};
int32_t main(int32_t argc, char** argv, char** envp)
{
char* const init_state_ptr = &init_state;
char state[0x36];
char* state_ptr = &state;
for (int64_t size = 0x36; size != 0; size -= 1)
{
*state_ptr = *init_state_ptr;
state_ptr += 1;
init_state_ptr += 1;
}
printf("Password: ", init_state_ptr);
fflush(stdout);
char input[0x18];
scanf("%24s", &input);
int64_t state_index = 0;
while (true)
{
if (strlen(&input) <= state_index)
{
// Cutting everything that happens
...
if (check == OK)
{
puts("Win!");
FILE file = fopen("flag.txt", &rb);
if (file != NULL)
{
char flag[0x46];
fread(&flag, 1, 0x46, file);
fclose(file);
puts(flag);
return 0;
}
else
puts("Send your input on the remote se…");
}
else
puts("Nope!");
break;
}
else
{
char* pos_ptr = strchr("abcdefghjklmnpqrstuvwxyz", input[state_index]);
if (pos_ptr != NULL)
{
// Doing stuff while iterating on the input
...
state_index += 1;
continue;
}
}
puts("Nope!");
break;
}
exit(1);
/* no return */
}
So I cleared everything so you can understand the structure of the code. It is really simple:
- First the program copies
0x36bytes from the init_state array to a local array - It then prompts for the password, asking for a maximum of 24 bytes
- Initialize an index that will be used to iterate over the input in an infinite loop
- We have 2 clear parts in this loop:
- The first one when we are done iterating on the input: We will go back to what this does later but we can clearly see that it performs the final check and prints us the flag if we are good.
- The second one is the part that iterates on the input, so the one that is executed first. We can also see that it matches the characters from our input against lower case letters, instantly exiting the program if it isn’t one
A first look at the init state shows us that it only contains only numbers
between 0x0 and 0xf, a good hint that it may be used to index an array of 0x10
elements.
Permutations on the state
Let’s start by looking inside that else block since it is the one doing stuff
with our input.
Ok so first thing you need to notice: you may think that characters are matched
on all lowercase letters but if you look closely, the 'i' and the 'o'
are missing, thus giving us an alphabet of 24 elements.
I know what you are thinking "But that's also the total size of the input, so characters from the input are used to index said input", yeah that could have
been a good idea, but it doesn’t do that and it is simply a coincidence.
So anyway we recover the index of the character in the alphabet and divide it by 4. The remainder is kept for later and the quotient is used to index a permutations matrix, which holds 6 permutation tables of 0x36 elements each.
The permutation matrix is linearized though so I already redefined the
dimesions so that’s why it’s showing really nicely in the code below. But to
know the dimensions I basically saw that the permutation matrix was indexed by
(pos / 4) * 0x36, since our alphabet holds 24 characters, that gives us 24 / 4 == 6 arrays of size 0x36 in the matrix. We can confirm the 0x36 because we
will iterate over 0x36 elements of the permutation array right after this.
We then copy the state and apply the permutations given by the fetched
permutation array. We repeat this process N times, N being pos % 4. We do not
actually really care about the copy, it is simply there as temporary buffer so
that permutations don’t cancel each other or erase data in the state, it is
just an implementation detail.
So to sum this up, each character from our input will chose a permutation array to apply to our state and how many times to apply the permutation. They are 6 permutations table possibles, and we can apply the same permutation between 0 and 3 times with a single input character.
So basically our input controls how we will shuffle the initial state.
You can also see right bellow the code a sample of the permutations matrix,
values seem really arbitrary but let’s see if you can already get a feeling of
what this is doing, I will explain it after understanding the entire if block
containing the final check.
else
{
char* pos_ptr = strchr("abcdefghjklmnpqrstuvwxyz", input[state_index]);
if (pos_ptr != NULL)
{
int64_t pos = pos_ptr - "abcdefghjklmnpqrstuvwxyz";
int32_t remainder = pos % 4;
char* permutation_array = &permutations[pos / 4];
while (true)
{
if (remainder < 1)
break;
remainder -= 1;
char state_copy[0x36];
char* state_copy_ptr = &state_copy;
char* state_ptr_1 = &state;
int64_t i = 0x36;
for (; i != 0; i -= 1)
{
*state_copy_ptr = *state_ptr_1;
state_copy_ptr += 1;
state_ptr_1 += 1;
}
do
{
char elem = state_copy[permutation_array[i]];
state[i] = elem;
i += 1
} while (i != 0x36);
}
state_index += 1;
continue;
}
}
And here a sample of the permutation matrix, telling you where each index of the state is going to be moved.
char permutations[0x6][0x36] =
{
[0x0] =
{
[0x00] = 0x09
[0x01] = 0x01
[0x02] = 0x02
[0x03] = 0x0c
[0x04] = 0x04
[0x05] = 0x05
[0x06] = 0x0f
[0x07] = 0x07
[0x08] = 0x08
[0x09] = 0x2d
...
[0x34] = 0x34
[0x35] = 0x35
}
[0x1] =
{
[0x00] = 0x00
[0x01] = 0x01
[0x02] = 0x2a
[0x03] = 0x03
...
[0x34] = 0x34
[0x35] = 0x11
[0x2] =
{
[0x00] = 0x02
[0x01] = 0x05
...
[0x35] = 0x35
}
[0x3] =
{
[0x00] = 0x00
[0x01] = 0x01
...
[0x35] = 0x33
}
[0x4] =
{
[0x00] = 0x00
[0x01] = 0x01
...
[0x35] = 0x35
}
[0x5] =
{
[0x00] = 0x21
[0x01] = 0x1e
...
[0x35] = 0x14
}
}
State checker
OK so the first part shuffled the state, so now I guess this simply checks if the resulting shuffled state is valid.
This one may be kind of tricky if you want to understand the implementations details, if you don’t care you can just skip right when I will recap what the puzzle actually is.
So I already renamed everything to keep it clear, I invite you to follow the code and its explanations a bit lower in parallel.
if (strlen(&input) <= state_index)
{
int64_t board = 0x3da8e0915f2c4b67;
int64_t next_board;
int64_t i = 0;
uint64_t move;
while (true)
{
uint64_t c = state[i];
void* allowed_moves = &allowed_moves;
int32_t shifter = 0x3c;
do
{
if (c == ((board >> shifter) & 0xf))
{
uint64_t* moves = allowed_moves;
do
{
move = *moves;
if (move == 0)
break;
moves += 1;
} while (((move * 0xf) & board) != 0);
if (move != 0)
break;
}
shifter -= 4;
allowed_moves += 0x28;
} while (shifter != 0xfffffffc);
if (c != ((board >> shifter) & 0xf) || move == 0)
break;
int64_t swapper = ((c * move) ^ (c << shifter));
next_board = (board ^ swapper);
if (board == swapper)
break;
i += 1;
if (i == 0x36)
break;
board = next_board;
}
if (next_board == 0x123456789abcdef0)
{
puts("Win!");
FILE file = fopen("flag.txt", &rb);
if (file != NULL)
{
char flag[0x46];
fread(&flag, 1, 0x46, file);
fclose(file);
puts(flag);
return 0;
}
else
puts("Send your input on the remote se…");
}
else
puts("Nope!");
break;
}
Basically you start with a board represented as an uint64_t intialized at
0x3da8e0915f2c4b67. For now, view this board as an array of 16 elements, each element being 4 bits (4 * 16 = 64).
As you know 4 bits is a single hexadecimal digit, so actually each hexadecimal
digit from this board is an element, so the initial board is:
[3, d, a, 8, e, 0, 9, 1, 5, f, 2, c, 4, b, 6, 7]
You may have noticed that every element is unique, they represent the entire range of numbers between 0x0 and 0xf, this is no coincidence.
We then create some variables that we will ignore for now, and an index (i)
that will be used to iterate over the state that was shuffled in the first part.
While iterating on the state, we fetch the current byte from the state, extended
to 64 bits. Remember how we told that state only held values between 0 and
0xf at the beginning ? Good, you are starting to see a pattern.
We create a pointer to a variable I called allowed_moves, it is once again a
two dimensionnal array because we iterate over it in a nested loop. I knew its
dimensions because this is the part to go to the next sub-array:
allowed_moves += 0x28;
So I knew each sub-array is 0x28 bytes, and I saw that the index used to
iterrate the outer loop is the shifter variable, initialized to 0x3c and
decremented by 4 each loop until it is strictly negative, so a total of 0x10
iterations. We then have a matrix containing 0x10 arrays of 0x28 bytes.
I also knew that the 0x28 bytes corresponded to 5 uint64_t since the inner
loop iterate over an uint64_t *
I pasted the entire content of this matrix below so you can have a look, you
will see that every element of this matrix has a single bit set to 1, and bits that are all sets at a position of 0 % 4 for that matter.
Okay let’s take a look at the shifter. It is initialized to 0x3c and is used
to shift the board, before keeping only the lowest weight hex-digit with the
& 0xf. The hex digit is then compared against the byte we fetched from our
state. If they differ, we basically skip this loop, decrementing the shifter
by 4 (meaning that on the next iteration we will select the next hex digit of
the board), and go to the next array in the allowed_moves matrix.
So to recap this, if you consider the board as an array of 4 bits elements,
shifter is actually an index used to iterate over this array. So we are
iterating to find at which index is the byte from the state inside the
board. allowed_moves will follow the same iterations, meaning that we will
select an allowed_moves sub-array based on where the state byte is located
in the board.
Good, so once we find our state byte inside board we start iterating over
the allowed_moves, basically the move is multiplied by 0xf, which will
effectively set the 4 bits corresponding to the single bit in the initial move,
this will now be used as a mask on the board.
So this move simply selects an hex digit from the board actually, if the
selected byte is NOT 0, then we continue the loop, skipping the move, but if it
is 0, then we exit the loop. Final check to see if the move itself was not 0, if
it is then we go back to trying the next shifter and allowed_moves, if not
then gg we selected a move. If at the end, no move was selected we go out of the
loop and basically lose.
So whatever this means, a valid move from a certain position in the board, must
match with the 0 digit from the board being at certain indexes, which, for
now, since we did not dig up the allowed_moves matrix yet, feel kind of arbitrary.
Feeling confused ? Don’t worry it will soon make sense.
uint64_t allowed_moves[0x10][0x5] =
{
[0x0] =
{
[0x0] = 0x0100000000000000
[0x1] = 0x0000100000000000
[0x2] = 0x0000000000000000
[0x3] = 0x0000000000000000
[0x4] = 0x0000000000000000
}
[0x1] =
{
[0x0] = 0x1000000000000000
[0x1] = 0x0010000000000000
[0x2] = 0x0000010000000000
[0x3] = 0x0000000000000000
[0x4] = 0x0000000000000000
}
[0x2] =
{
[0x0] = 0x0100000000000000
[0x1] = 0x0001000000000000
[0x2] = 0x0000001000000000
[0x3] = 0x0000000000000000
[0x4] = 0x0000000000000000
}
[0x3] =
{
[0x0] = 0x0010000000000000
[0x1] = 0x0000000100000000
[0x2] = 0x0000000000000000
[0x3] = 0x0000000000000000
[0x4] = 0x0000000000000000
}
[0x4] =
{
[0x0] = 0x1000000000000000
[0x1] = 0x0000010000000000
[0x2] = 0x0000000010000000
[0x3] = 0x0000000000000000
[0x4] = 0x0000000000000000
}
[0x5] =
{
[0x0] = 0x0100000000000000
[0x1] = 0x0000100000000000
[0x2] = 0x0000001000000000
[0x3] = 0x0000000001000000
[0x4] = 0x0000000000000000
}
[0x6] =
{
[0x0] = 0x0010000000000000
[0x1] = 0x0000010000000000
[0x2] = 0x0000000100000000
[0x3] = 0x0000000000100000
[0x4] = 0x0000000000000000
}
[0x7] =
{
[0x0] = 0x0001000000000000
[0x1] = 0x0000001000000000
[0x2] = 0x0000000000010000
[0x3] = 0x0000000000000000
[0x4] = 0x0000000000000000
}
[0x8] =
{
[0x0] = 0x0000100000000000
[0x1] = 0x0000000001000000
[0x2] = 0x0000000000001000
[0x3] = 0x0000000000000000
[0x4] = 0x0000000000000000
}
[0x9] =
{
[0x0] = 0x0000010000000000
[0x1] = 0x0000000010000000
[0x2] = 0x0000000000100000
[0x3] = 0x0000000000000100
[0x4] = 0x0000000000000000
}
[0xa] =
{
[0x0] = 0x0000001000000000
[0x1] = 0x0000000001000000
[0x2] = 0x0000000000010000
[0x3] = 0x0000000000000010
[0x4] = 0x0000000000000000
}
[0xb] =
{
[0x0] = 0x0000000100000000
[0x1] = 0x0000000000100000
[0x2] = 0x0000000000000001
[0x3] = 0x0000000000000000
[0x4] = 0x0000000000000000
}
[0xc] =
{
[0x0] = 0x0000000010000000
[0x1] = 0x0000000000000100
[0x2] = 0x0000000000000000
[0x3] = 0x0000000000000000
[0x4] = 0x0000000000000000
}
[0xd] =
{
[0x0] = 0x0000000001000000
[0x1] = 0x0000000000001000
[0x2] = 0x0000000000000010
[0x3] = 0x0000000000000000
[0x4] = 0x0000000000000000
}
[0xe] =
{
[0x0] = 0x0000000000100000
[0x1] = 0x0000000000000100
[0x2] = 0x0000000000000001
[0x3] = 0x0000000000000000
[0x4] = 0x0000000000000000
}
[0xf] =
{
[0x0] = 0x0000000000010000
[0x1] = 0x0000000000000010
[0x2] = 0x0000000000000000
[0x3] = 0x0000000000000000
[0x4] = 0x0000000000000000
}
}
Great, we now have a move which is the index of the 0 element of the board,
a shifter, being the index of the byte from our state in the same board. The
previous paragraph was meant to make sure this move/shifter association is
valid.
Let’s talk about the swapper now, it is composed of 2 parts:
-
c << shifter: so it will be the representation of the board as if onlycwas on it -
c * move: the representation of the board as ifcwas at the position indicated by the move, and no other element on the board. So it the board, with c at the position of the 0 and nothing else on the board
We then compute the next board by xoring the current one with the swapper.
This will have the effect to xor the current element of the state AND the
current 0 from the board with the current element of the state. This will
have the effect to actually swap the 0 and our element of the state.
And after that we simply go the next state byte, until we have done all 0x36
of them.
Let’s recap:
-
each character from the
stateselects the corresponding hex digit in the board. -
According to its position in the board, we will try to find a valid move, being a move that have
0as destination, but only certains positions of0are allowed according to were the hex digit was in the board. -
If a valid move was found, then we swap the
0and thestatebyte.
FINALLY, there is the final check, after all the moves from the state have been applied, the board must be 0x123456789abcdef0.
Great, now let’s look at the allowed_moves.
So what I did to understand what all those valid moves were was to take a pen,
drew an array of 16 elements, and for each element I drew an arrow to every
valid moves from that position. So just ignore that there has to be a 0 at
these positions for now, it’s simply a matter of “if there was a 0 there, could
I move here ?”. And it started looking like this for the first few elements:
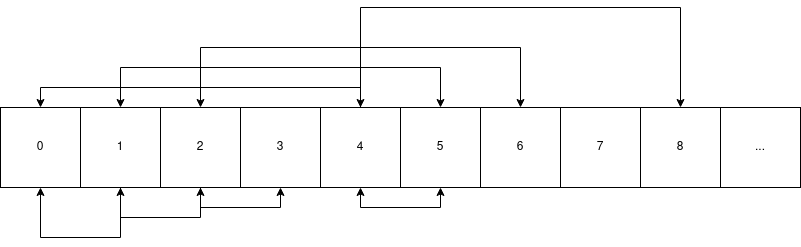
What you need to notice is that every move can be inverted, so you can go back to your position after moving. MOST tiles can go to the tiles right next to them or to the tiles that are 4 tiles farther. For example, tile at index 1 can go either at 0, 2, or 5. You are probably starting to understand, let’s just put the final touch: 3 cannot go to 4 and vise-versa.
So this is simply a flattened 4 * 4 grid, where you can only move to the
adjacent tiles. Let’s now replace the indexes I put in the diagram above with
the actual values of the initial board (0x3da8e0915f2c4b67) we have:
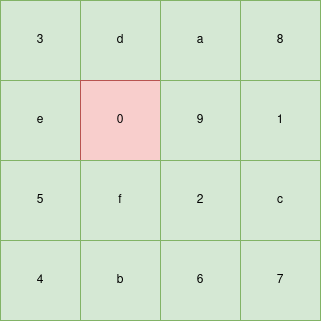
I know you understood everything but let’s just see the target board
(0x123456789abcdef0):
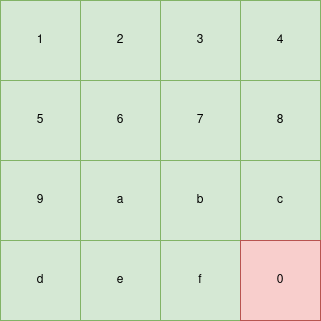
So we need to get from one to the other in 0x36 moves exactly, each move swapping the 0 with an adjacent tile.
Cool, all of this simply for a slide puzzle. Each element of the state corresponds to the tile that we must push on the 0 (which represents the empty tile in the slide puzzle). Let’s go and solve th…
But wait there was a first step
I hope you did not forget that the state used to select which tiles are moved in which order was shuffled by the first step according to our input.
Maybe it’s time to understand how this shuffle work.
OK so I got this one super fast actually, let’s just get you the context back:
- 6 permutations tables possibles
- each can be applied
[0;4[times each time 0x36 == 54elements in the state
If you are a puzzle fan you already know what this is I don’t even need to show you the permutation matrix again but hey:
char permutations[0x6][0x36] =
{
[0x0] =
{
[0x00] = 0x09
[0x01] = 0x01
[0x02] = 0x02
[0x03] = 0x0c
[0x04] = 0x04
[0x05] = 0x05
[0x06] = 0x0f
[0x07] = 0x07
[0x08] = 0x08
[0x09] = 0x2d
...
[0x34] = 0x34
[0x35] = 0x35
}
[0x1] =
{
[0x00] = 0x00
[0x01] = 0x01
...
Literally what I did is I saw the first permutation table, noticed that only 1 element out of 3 were moving (so I though this was a 3 * 3 array) and that the first ones were moving 9 tiles further than there original location (so probaly a 3 * 3 * 3 cube), oh wait did I say cube ? 6 faces ? can be rotated up to 3 times ? 54 elements ? yeah ok you got it aswell.
It’s a rubiks cube.
Each permutation table is a counter-clockwise rotation of a face of the cube.
The process of mapping the cube in its flattened representation and to know which permutations corresponds to which face is just teadious so I will just give you this one out.
Do keep in mind that I was not familiar with standard rubiks cube notations, so I named a move by the color of the face that is rotating instead of the usual U,F,… it felt more intuitive to me.
Here are the indexes of each cube tile on the flatenned state:
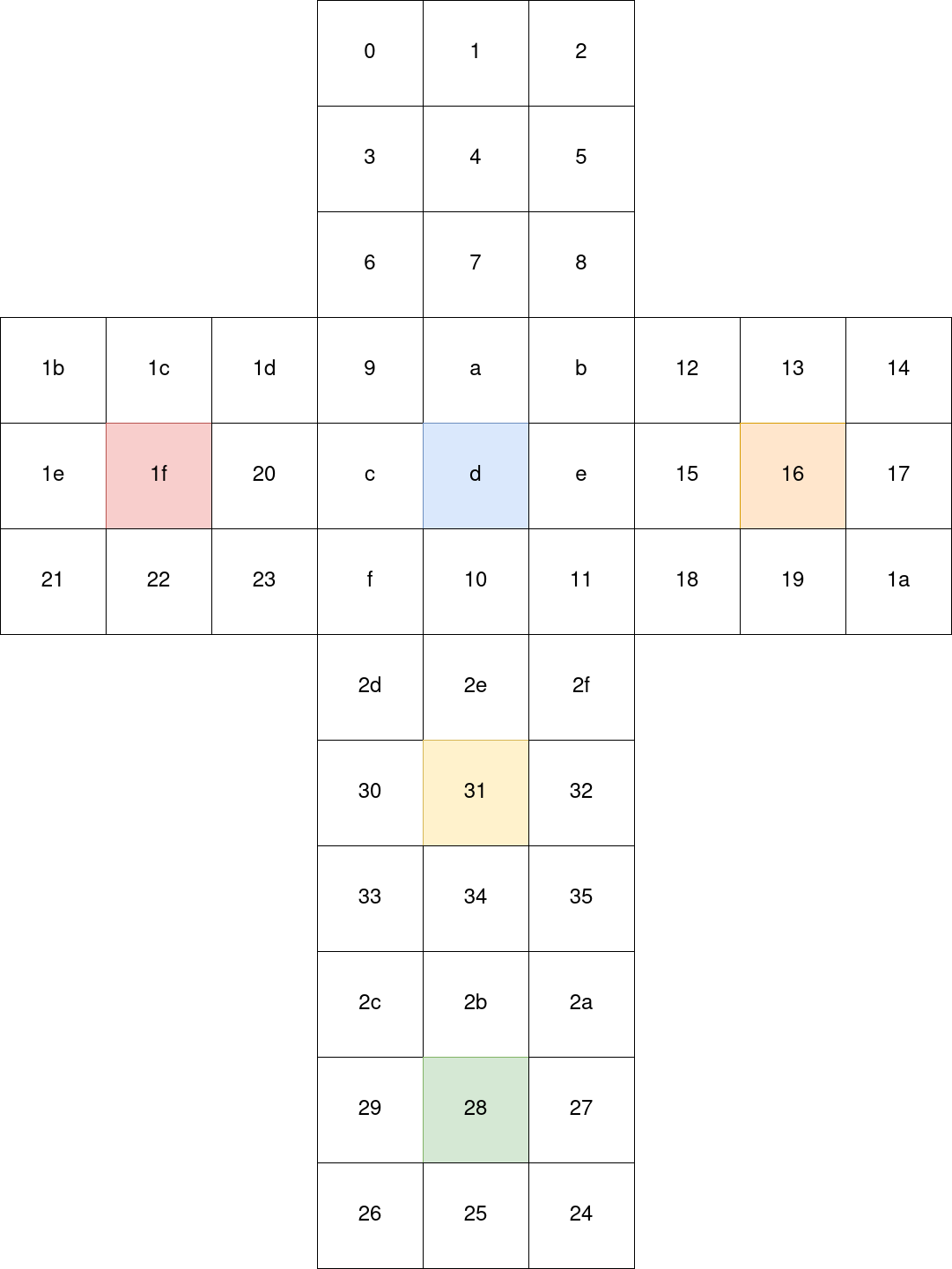
I attributed colors to faces arbitrarily to respect the usual cube configuration, but as long as I keep everything coherent with this representation I will do just fine.
With the above cube, fold it back and see how the first permutation array indeed performs a counter-clockwise rotation of the red face.
Here is the initial state of the cube:
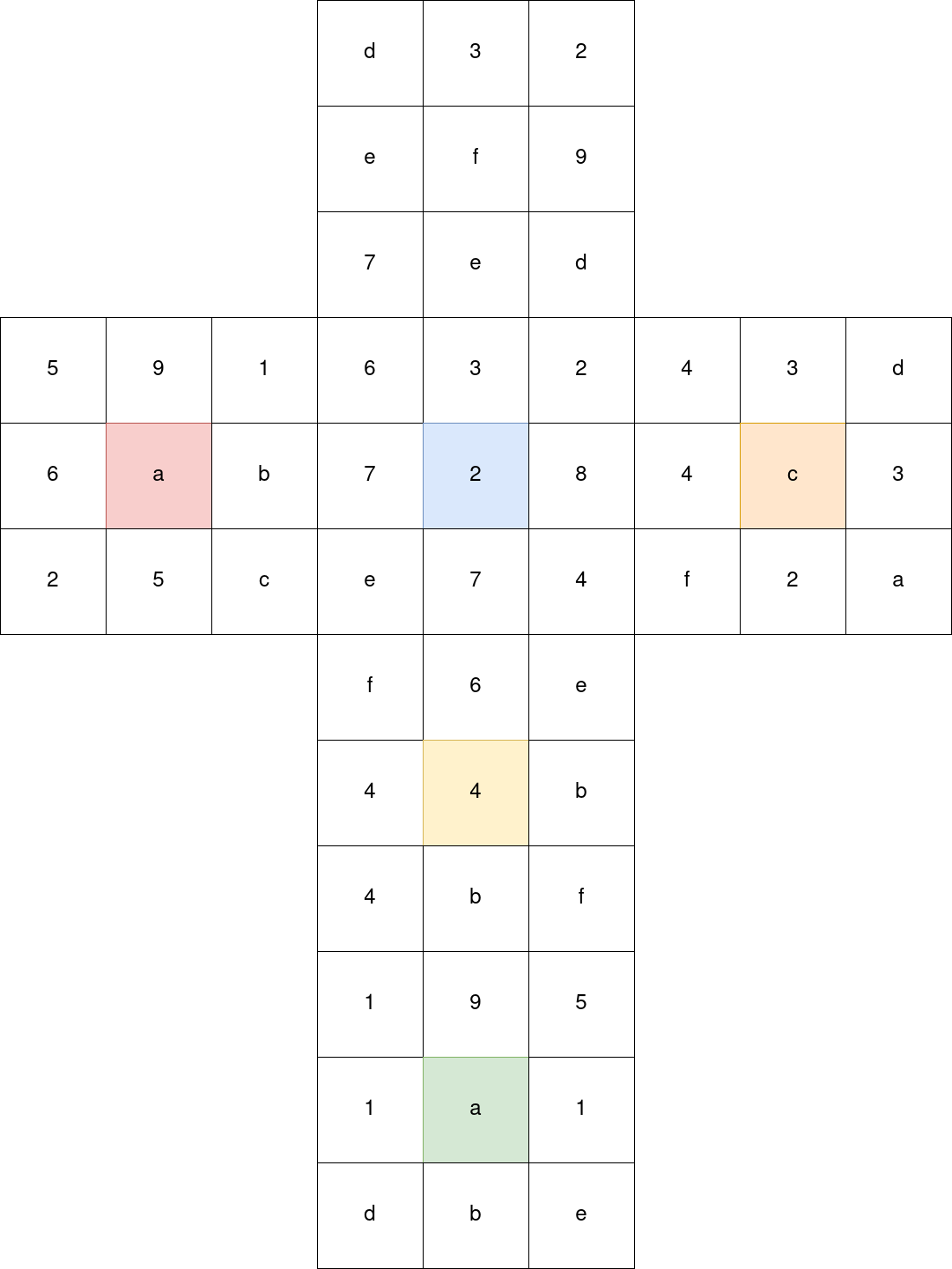
Solving the slide puzzle
Recap everything
So now we are done with the reversing part. With our input, the program will:
- Consider each character as a move on a rubiks cube, applying said move
- Consider the flatenned shuffled cube as a list of slide puzzle moves
Basically we need to solve a rubik’s cube in order to ordonate a slide puzzle solution.
To solve this, we will need to take one problem at a time, first find a solutions to the slide puzzle, then map the solution to a cube which we will consider as the solved cube, then map the color of the solved cube back to the starting cube in order to solve it.
Naive backtracking
So to start I want to say that I am really impressed that the solver of
face0xff found a solution this fast, I was really convinced that without the
little tricks that I will show you, it would take too long to search for a 54
moves solution, but hey seems like it works if you implement every slide puzzle
heuristics you may think of.
So my approach was a backtracking algorithm, however you can clearly see why backtracking 54 moves is not a good solution so we will need to add some heuristics to narrow down the search for valid moves.
Basically the algorithm works as follow given a current state of the grid:
- If the puzzle is solved it’s won
- If you have no move left it’s lost
- generate all possible moves
- try each move by applying the move and recursively calling this procedure
- if the recursive call returned true then it’s won
- else cancel the move and try the next
- if no move returned true there is no solution
Slide puzzle heuristics
Okay this algorithm will take way too long, we need to cancel some search paths early so that we will not further go down the calls if we can already know that we cannot solve anymore from a given grid.
Cannot cancel previous move
This heuristic takes the assumption that you cannot play the same move as the previous one, because otherwise you will go back to same state as the previous move, effectively doing 2 moves for nothing.
Okay this heuristic is not exactly 100% reliable, since actually the puzzle is
also solvable this way, simply with useless moves. But I was convinced that 54
was the optimal solution, I don’t imagine that \J would have asked us to solve
a puzzle in a non-optimal way.
Last move
Since the tile in bottom right needs to be 0, this means that the last move
needs to be f or c, so if at any point, both of these tiles do not have
anymore remaining moves while the puzzle isn’t already solved then you can
already tell it’s unsolvable.
Oh I didn’t talk about the limited number of moves per tiles ? Don’t worry I’ll explain in a minute.
Rubik’s cube heuristics
These are the heuristics you can determine based on the fact that the moves are shuffled from a rubik’s cube initial state.
Face centers
In a rubik’s cube the center tile of each face CANNOT move, this means that since we know the starting position of the cube, we already know that:
- Move
4will bef - Move
dwill be2 - Move
16will bec - Move
1fwill bea - Move
28will bea - Move
31will be4
Move counts and manhattan distance
Of course I kept the best one for the end, this is by far the most effective one and it is probably enough to solve the whole thing by itself.
This heuristic is based on the fact that we can only shuffle the cube, we can
never add or remove moves, therefore we can know how many times a tile will be
moved. For example there are 4 1 on the cube, so this means that the 1 tile
of the slide puzzle must be played exactly 4 times, no more no less.
So now, knowing this, while backtracking, we can keep track of how many times a tile has moved by decrementing its move counter.
Then, we can compute the manhattan distance of the tile to its supposed
location, which is the minimum number of moves that would be required for the
tile to go to that location if there were no other tile on the grid. For example
tile f placed in the top left corner will have a manhattan distance of 5 to
its supposed location.
So whenever the move counter of a tile becomes lower than its manhattan distance to its supposed location, you know that you will never be able to place the tile back to where it is supposed to be.
Solver
So I implemented this in rust because I wanted this to be fast:
use std::collections::HashMap;
struct Board {
board: [usize; 0x10],
moves: Vec<usize>,
max_moves: usize,
move_number: usize,
empt_idx: usize,
solved_grid: [usize; 0x10],
fixed_moves: HashMap<usize, usize>,
move_limit: [isize; 0x10]
}
impl Board {
pub fn new(board: [usize; 0x10]) -> Self {
let empt_idx: usize = board.iter().position(|&r| r == 0).unwrap().try_into().unwrap();
let all_moves: [usize; 0x36] = [
0x0d, 0x03, 0x02, 0x0e, 0x0f, 0x09, 0x07, 0x0e, 0x0d, 0x06, 0x03, 0x02, 0x07, 0x02, 0x08, 0x0e,
0x07, 0x04, 0x04, 0x03, 0x0d, 0x04, 0x0c, 0x03, 0x0f, 0x02, 0x0a, 0x05, 0x09, 0x01, 0x06, 0x0a,
0x0b, 0x02, 0x05, 0x0c, 0x0e, 0x0b, 0x0d, 0x01, 0x0a, 0x01, 0x05, 0x09, 0x01, 0x0f, 0x06, 0x0e,
0x04, 0x04, 0x0b, 0x04, 0x0b, 0x0f
];
let solved_grid: [usize; 0x10] = [1,2,3,4,5,6,7,8,9,0xa,0xb,0xc,0xd,0xe,0xf,0];
let mut fixed_moves: HashMap<usize, usize> = HashMap::new();
for i in vec![4, 0xd, 0x16, 0x1f, 0x28, 0x31] {
fixed_moves.insert(i, all_moves[i]);
}
let mut move_limit: [isize; 0x10] = [0; 0x10];
for mv in all_moves.iter() {
move_limit[*mv] += 1;
}
Board {
board: board,
moves: Vec::new(),
max_moves: 0x36,
move_number: 0,
empt_idx: empt_idx,
solved_grid: solved_grid,
fixed_moves: fixed_moves,
move_limit: move_limit,
}
}
pub fn solved(&self) -> bool {
self.board == self.solved_grid
}
pub fn get_move(&self, off: Vec<isize>) -> Option<usize> {
let empt_idx: isize = self.empt_idx.try_into().unwrap();
let empt_i: isize = empt_idx / 4;
let empt_j: isize = empt_idx % 4;
let src_i: isize = empt_i + off[0];
let src_j: isize = empt_j + off[1];
if src_i < 4 && src_i >= 0 && src_j < 4 && src_j >= 0 {
let idx: usize = (src_i * 4 + src_j).try_into().unwrap();
return Some(self.board[idx])
}
None
}
pub fn generate_moves(&self) -> Vec<usize> {
let mut moves: Vec<usize> = Vec::new();
for off in vec![vec![-1, 0], vec![1, 0], vec![0, -1], vec![0, 1]] {
let maybe_move = self.get_move(off);
if let Some(mv) = maybe_move {
moves.push(mv);
}
}
moves
}
pub fn apply_move(&mut self, mv: usize, undo: bool) {
let i: usize = self.board.iter().position(|&x| x == mv).unwrap();
let tmp: usize = self.board[i];
self.board[i] = self.board[self.empt_idx];
self.board[self.empt_idx] = tmp;
self.empt_idx = i;
if undo {
self.move_number -= 1;
self.moves.pop();
self.move_limit[mv] += 1;
}
else {
self.move_number += 1;
self.moves.push(mv);
self.move_limit[mv] -= 1;
}
}
pub fn manhattan_distance(&self, mv: usize) -> isize {
let mv_idx: isize = self.board.iter().position(|&x| x == mv).unwrap().try_into().unwrap();
let mv_i: isize = mv_idx / 4;
let mv_j: isize = mv_idx % 4;
let supposed_idx: isize = (mv - 1).try_into().unwrap();
let supposed_i: isize = supposed_idx / 4;
let supposed_j: isize = supposed_idx % 4;
let manhattan: isize = (supposed_j - mv_j).abs() + (supposed_i - mv_i).abs();
manhattan
}
pub fn solve(&mut self) -> bool {
// GG
if self.solved() {
return true;
}
// No more moves
if self.move_number >= self.max_moves {
return false;
}
// Last move need to be 0xc or 0xf
if self.move_limit[0xc] <= 0 && self.move_limit[0xf] <= 0 {
return false;
}
let last_move: Option<usize> = self.moves.last().copied();
if let Some(mv) = last_move {
// Tile cannot possibly go back to its supposed location
let man: isize = self.manhattan_distance(mv);
if self.move_limit[mv] < man {
return false
}
}
// Generate possible moves from current grid
let mut moves: Vec<usize> = self.generate_moves();
// Cannot apply same move twice
if let Some(mv) = last_move {
moves = moves.iter().filter(|&x| *x != mv).cloned().collect();
}
// Filter fixed moves from the cube center tiles
if self.fixed_moves.contains_key(&self.move_number) {
let mv: usize = *self.fixed_moves.get(&self.move_number).unwrap();
moves = moves.iter().filter(|&x| *x == mv).cloned().collect();
}
for mv in moves {
// Apply move
self.apply_move(mv, false);
// Recursive call
let solved: bool = self.solve();
// GG
if solved {
return true;
}
// Undo move
self.apply_move(mv, true);
}
false
}
}
fn solve() {
let arr: [usize; 0x10] = [
3, 0xd, 0xa, 8,
0xe, 0, 9, 1,
5, 0xf, 2, 0xc,
4, 0xb, 6, 7
];
let mut board: Board = Board::new(arr);
board.solve();
println!("{:x?}", board.moves);
}
fn main() {
solve()
}
And guess what ? It was super duper fast:
$ time cargo run --release
Finished release [optimized] target(s) in 0.00s
Running `target/release/picasso`
[e, 5, 4, b, f, e, d, 3, 5, 4, e, d, 9, 2, 6, f, b, e, d, 9, 2, 1, c, 7, f, b, e, d, 9, 2, 1, a, 3, 1, 4, 5, 1, 4, 2, 6, a, 3, 4, 2, 6, a, 7, c, 8, 4, 3, 7, b, f]
________________________________________________________
Executed in 77.37 millis fish external
usr time 71.83 millis 182.00 micros 71.65 millis
sys time 3.93 millis 673.00 micros 3.26 millis
That shit is probably completely overengineered and I don’t care, I had fun writing it.
I checked manually that this solution was correct and moved to the next step.
Solving the rubik’s cube
We now have our solution for the slide puzzle, so let’s map it as a solved rubik’s cube, we know the mapping using the index cube net which gives us which tiles of the cube corresponds to which move index on the slide puzzle:
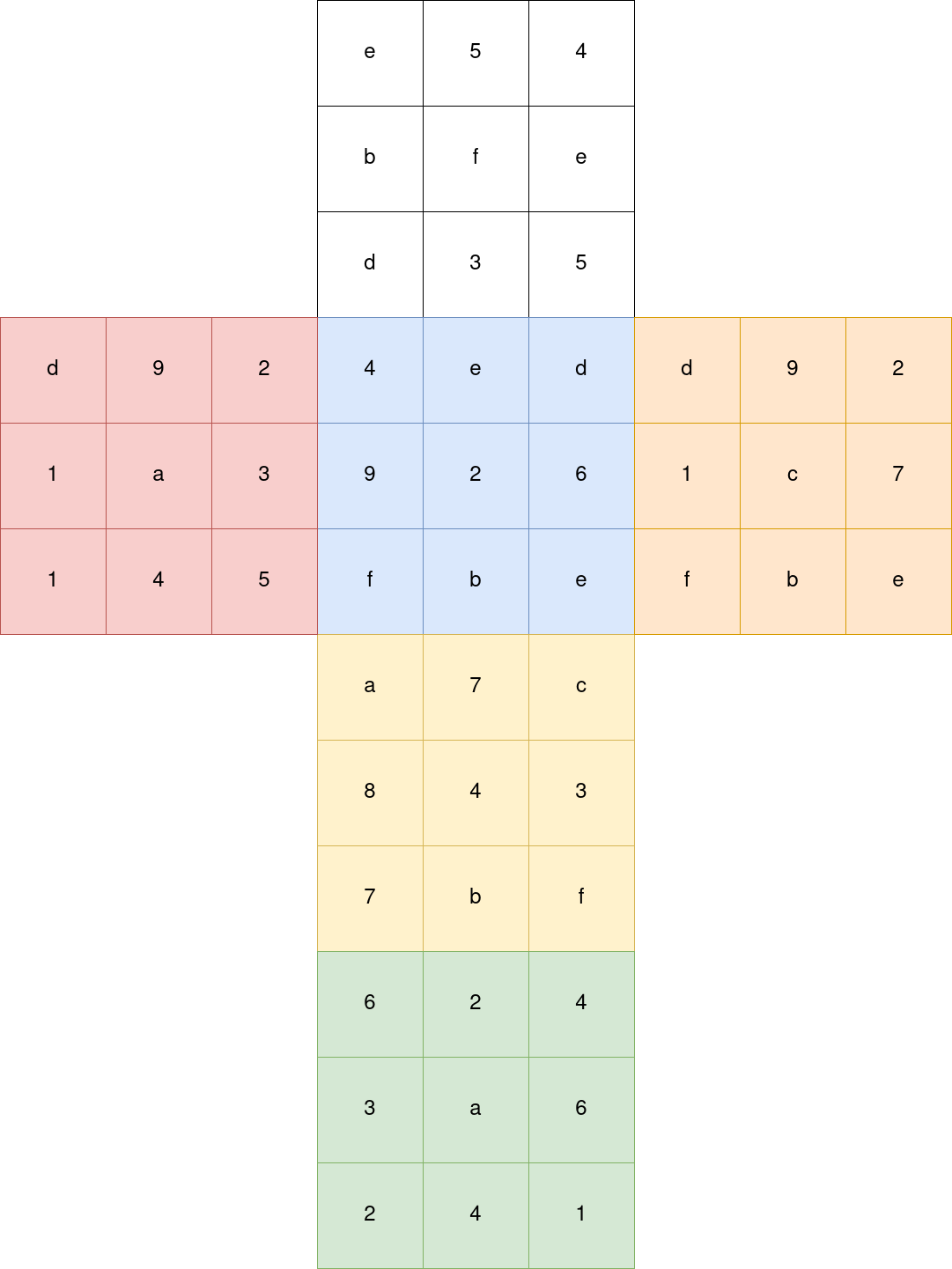
Since this is the solved cube, we attribute all the colors of the tiles.
We now need to attribute the corresponding colors to the initial state of the cube so that we can input a valid cube to a solver.
To do this, we use the fact that tiles that are connected along an edge or a corner will always be linked, so this way we can identify the tile groups on the cube and identify their color from the solved cube.
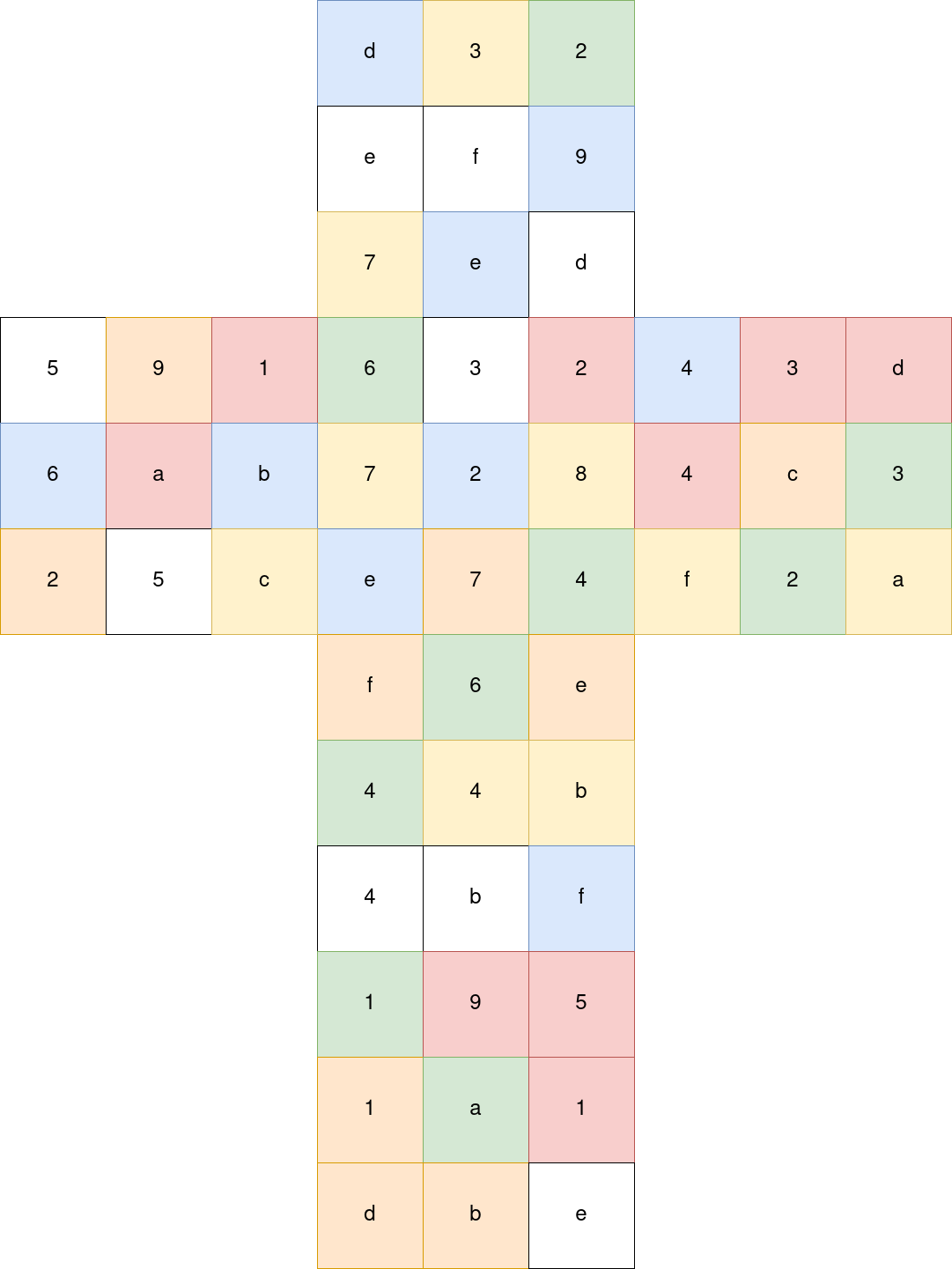
Then I basically just used this online solver, put manually all the colors, clicked on solve, and the site instantly found a solution in 22 moves. So I noted manually every move, which face was supposed to move and wrote a script that mapped the moves back to the expected input of the program.
In the script ('g', 2) means rotate the green face 2 times, ('o', 3) means rotate the orange face 3 times counter-clock wise …
#!/usr/bin/env python3
import os
alphabet = b"abcdefghjklmnpqrstuvwxyz"
moves = [
('g', 2),
('o', 3),
('g', 3),
('b', 2),
('y', 2),
('g', 3),
('w', 1),
('o', 3),
('r', 3),
('y', 1),
('r', 3),
('w', 1),
('b', 1),
('o', 2),
('g', 1),
('y', 2),
('g', 1),
('y', 2),
('r', 2),
('g', 2),
('w', 2),
('o', 2),
]
sequence = b""
def face_id(face):
res = 0
if face == 'w':
res = 2
if face == 'b':
res = 4
if face == 'o':
res = 1
if face == 'r':
res = 0
if face == 'y':
res = 3
if face == 'g':
res = 5
return res
for move in moves:
i = face_id(move[0]) * 4 + move[1]
sequence += alphabet[i].to_bytes(1, "little")
os.write(1, sequence + b'\n')
And piping this script in the program indeed gets us the flag.
$ ./solve.py | ./picasso
Password: Win!
Send your input on the remote service to retrieve the flag.
$ ./solve.py | nc challenges.france-cybersecurity-challenge.fr 2251
Password: Win!
FCSC{235b605a121bdd4b09adc4823bdf0967c446647c1ec69234813068a916fd83a6}