Inverting a bunch of matrices because reverse engineering or something | Brachiosaure @ FCSC 2023
Intro
Brachiosaure is a math/puzzle challenge from \J for the 2023 edition of the
FCSC. It’s difficulty is not in the reversing process, which is fairly trivial
here, but in solving the underlying problem.

Challenge description
reverse | 477 pts 10 solves ⭐⭐
Vous aimez les QR Codes ? On vous demande d'écrire un générateur d'entrées
valides pour ce binaire, puis de le valider sur le service web fourni où un nom
aléatoire est proposé toutes les 5 secondes.
Author: \J
Given files
Writeup
Overview
As we can guess from the challenge description, this binary will take images as input. QR codes images for that matter.
$ file brachiosaure
brachiosaure: ELF 64-bit LSB pie executable, x86-64, version 1 (SYSV),
dynamically linked, interpreter /lib64/ld-linux-x86-64.so.2, BuildID[sha1
=3e4d225f1053b2a64de1cd133563e6e655049aca, for GNU/Linux 3.2.0, stripped
$ ldd brachiosaure
linux-vdso.so.1 (0x00007ffd833bd000)
libzbar.so.0 => /usr/lib/libzbar.so.0 (0x00007f3ec2325000)
libpng16.so.16 => /usr/lib/libpng16.so.16 (0x00007f3ec22ec000)
libcrypto.so.1.1 => /usr/lib/libcrypto.so.1.1 (0x00007f3ec1fff000)
libc.so.6 => /usr/lib/libc.so.6 (0x00007f3ec1e18000)
libdbus-1.so.3 => /usr/lib/libdbus-1.so.3 (0x00007f3ec1dc7000)
libv4l2.so.0 => /usr/lib/libv4l2.so.0 (0x00007f3ec1db8000)
libX11.so.6 => /usr/lib/libX11.so.6 (0x00007f3ec1c73000)
libXv.so.1 => /usr/lib/libXv.so.1 (0x00007f3ec1c6b000)
libjpeg.so.8 => /usr/lib/libjpeg.so.8 (0x00007f3ec1be8000)
libz.so.1 => /usr/lib/libz.so.1 (0x00007f3ec1bce000)
libm.so.6 => /usr/lib/libm.so.6 (0x00007f3ec1ae6000)
/lib64/ld-linux-x86-64.so.2 => /usr/lib64/ld-linux-x86-64.so.2 (0x00007f3ec23a2000)
libsystemd.so.0 => /usr/lib/libsystemd.so.0 (0x00007f3ec1a09000)
libv4lconvert.so.0 => /usr/lib/libv4lconvert.so.0 (0x00007f3ec198e000)
libxcb.so.1 => /usr/lib/libxcb.so.1 (0x00007f3ec1963000)
libXext.so.6 => /usr/lib/libXext.so.6 (0x00007f3ec194e000)
libcap.so.2 => /usr/lib/libcap.so.2 (0x00007f3ec1942000)
libgcrypt.so.20 => /usr/lib/libgcrypt.so.20 (0x00007f3ec17fa000)
liblzma.so.5 => /usr/lib/liblzma.so.5 (0x00007f3ec17c7000)
libzstd.so.1 => /usr/lib/libzstd.so.1 (0x00007f3ec16f5000)
liblz4.so.1 => /usr/lib/liblz4.so.1 (0x00007f3ec16d3000)
libgcc_s.so.1 => /usr/lib/libgcc_s.so.1 (0x00007f3ec16b3000)
libXau.so.6 => /usr/lib/libXau.so.6 (0x00007f3ec16ae000)
libXdmcp.so.6 => /usr/lib/libXdmcp.so.6 (0x00007f3ec16a6000)
libgpg-error.so.0 => /usr/lib/libgpg-error.so.0 (0x00007f3ec1680000)
That’s a lot of libraries, this is really good news because we can just look up the documentation of those libraries to understand what is going on.
The most important ones are libpng to read the image data and libzbar which
is used to read data from a QR code. Turns out symbols are really self
explanatory by themselves, the code basically reads like sources even though it
is stripped.
By executing it, we can already what the program is expecting: a username, and two png, one for the username and one for the serial, probably QR codes encoding said username and its serial.
$ ./brachiosaure
Usage: ./brachiosaure <username> <username.png> <serial.png>
So is this just a simple keygen that needs to output its key as a QR code ? (Spoiler it isn’t)
Reversing
Main
I’m saving you the trouble of renaming the variables, the function I called
get_qr_data reads like a charm. It basically is just a succession of calls to
libpng and libzbar, it does exactly what you think it does, reads an image
file, decode the QR code it contains and outputs everything in the pointers
passed as parameters so I won’t show the process of reversing it.
The only thing worth pointing is that it grayscales the input image.
int32_t main(int32_t argc, char** argv, char** envp) __noreturn
{
int32_t user_status;
int32_t serial_status;
int32_t status;
if (argc == 4)
{
int32_t user_width = 0;
int32_t user_height = 0;
void* username_img_data = NULL;
void* user_zbar_img = NULL;
int32_t serial_width = 0;
int32_t serial_height = 0;
void* serial_img_data = NULL;
void* serial_zbar_img = NULL;
char digest[0x40];
strcpy(&digest, argv[1]);
void sha512;
SHA512_Init(&sha512);
SHA512_Update(&sha512, &digest, strlen(argv[1]));
SHA512_Final(&digest, &sha512);
char qr_data_user[0x40];
user_status = get_qr_data(argv[2],
&username_img_data,
&user_width,
&user_height,
&user_zbar_img,
&qr_data_user,
0x40);
char qr_data_serial[0x40];
serial_status = get_qr_data(argv[3],
&serial_img_data,
&serial_width,
&serial_height,
&serial_zbar_img,
&qr_data_serial,
0x40);
if ((user_status != 0 && serial_status != 0))
{
char err = (serial_width != user_width)
| (serial_height != user_height)
| (user_width != user_height)
| (memcmp(&digest, &qr_data_user, 0x40) != 0)
| (check_serial(&qr_data_user, &qr_data_serial, 8) == 0);
void* an_interesting_output = NULL;
int32_t win = something_interesting(username_img_data, serial_img_data, &an_interesting_output, user_width);
free(username_img_data);
free(serial_img_data);
free(an_interesting_output);
status = err | (win == 0);
}
}
else
{
printf("Usage: %s <username> <username.p…", *argv);
}
if (argc != 4 || user_status == 0 || serial_status == 0)
{
status = 1;
}
exit(status);
/* no return */
}
So we compute the sha512 of the username, this gives us a digest, that we will
keep for later, just remember that we have this digest of the username.
We then decode the 2 QR codes, both seem to need to encode 0x40 bytes of data.
(I know you already guessed it, a sha512 is also 0x40 bytes long).
And finally we perform some checks:
- Both pictures needs to be a square of the same size
- The encoded data of the user QR code needs to be equal to the user digest
- The serial check, taking both QR datas as input
- And finally a last check but this time taking both images data instead of the QR data.
check_serial
uint64_t check_serial(void* user_digest, int64_t serial, int32_t size)
{
void* buff = NULL;
int64_t res;
if (user_digest == NULL || serial == NULL)
return 0;
something_interesting(user_digest, user_digest, &buff, size);
res = memcmp(serial, buff, size * size) == 0;
free(buff);
return res;
}
Hmmm we find again the same interesting check that was performed in the main function, something is already interesting but let’s first note things that we can already guess from this:
Since it take our images as input in main and image width, it certainly
interprets the data as a linearized 2 dimensionnal array, taking the width as
parameter. We can confirm this since the check serial is called with size 0x8
as parameter and 0x8 * 0x8 == 0x40.
Now let’s see what is different:
// Inside check serial
something_interesting(user_digest, user_digest, &buff, size);
res = memcmp(serial, buff, size * size) == 0;
// Inside main
int32_t win = something_interesting(username_img_data, serial_img_data,
&an_interesting_output, user_width);
First the result is not used in the same way:
-
Inside
check_serial, the return value is discarded, and the output buffer is compared to the serial, so it is bascically a keygen, seems easy enough -
Inside
main, the output buffer is discarded and only the return value is checked
Then in the main, the function is called with the user and serial images data,
but in check_serial, it is called with the digest data twice.
OK let’s see what this does, we need to understand what doest it put in the output buffer since it will be the serial we will need to encode in the second QR code of the input, but we also need to understand the return value.
dot_product
Cutting drama right now, it is simply a matrix dot product:
uint64_t dot_product(char* A, char* B, char** out, int32_t size)
{
if (A == NULL || B == NULL)
{
return 0;
}
int32_t res = 1;
int64_t i = 0;
int32_t j = 0;
*out = calloc(size * size, 1);
while (size > j)
{
int64_t k = 0;
char* A_line = A + i;
do
{
char* B_col = B + k;
int64_t col = 0;
int32_t sum = 0;
do
{
char element;
element = A_line[col];
element *= B_col[0];
col += 1;
B_col += size;
sum += element;
} while (size > col);
((*out) + i)[k] = sum; // ith line, kth column
bool win;
if (j != k) // Check if on the diagonal
win = sum == 0; // if not check that it is 0
else
win = sum == 1; // if yes check it is 1
k += 1;
res &= win; // Bitwise and, every number must be correct
} while (size > k);
j += 1;
i += size;
}
return res;
}
Alright so to recap what actually happens:
-
In check serial, we perform the dot product of the user digest, interpreted as a linearized 8 * 8 matrix, with itself, effectively squaring it, which gives us our serial (also in a linearized 8 * 8 matrix).
-
In main, we perform the dot product of the user and serial IMAGES, and we can see from the code that the return value indicates wether or not the resulting dot product is the identity matrix.
So yeah, congratulation, it is the end of the reversing part.
We now need to, given a random username:
- Compute its digest
- Square it to get the serial
- Output both the digest and the serial to a QR code each
- (The fun part) Make sure that the images of said QR codes are invertible
Splitting the problem
So at first I though this was impossible, but I gradually had more and more tricks up my sleeve to solve this, which I finally almost all threw by the window when I discovered how easy the solver actually is.
I still think that even though completely over engineered and full of dead ends, my thought process may be of value for someone I guess.
Recontextualizing
So first we need to understand that we are not doing any kind of dot product and are not working with any kind of matrices.
Both only operate over the unsigned integers modulo 256, since the dot product
stores its output on a char. This will be the key to make the matrix
invertible.
You can then notice that in the fieds of integers modulo 256, 0xff * 0xff == 1. When I noticed I started to think that I could carefully place white pixels
on the QR code to specifically put some 1s where I wanted, but since patching a
single byte of the first/second matrix will impact the entire corresponding
row/column of the dot product, it doesn’t work obviously
Now, obviously we will need to patch the QR code image, the question is how much
so that libzbar still decodes the correct digests and serial. So obviously,
we may resize the images of the QR codes to add some data.
Dead end
So then this is where I had a really dumb idea. I thought that maybe I could append carefully crafted columns and empty lines to the first matrix, and carefully crafted line and empty columns to the second matrix so that the result of the dot product int overflow back to 0 or 1. Thus outputing 2 new images with the QR code in the top left corner.
And it actually kind of worked, but not entirely so I won’t detail the algorithm, I still implemented it entirely because I was really convincend this was the intended way.
Why it doesn’t work is because yes by adding rows and columns like that, being carefull that everything cancels nicely with the data you inject on the other matrix, the first N rows and columns of the original images have indeed been inverted, but now you have a matrix which is somewhat bigger, and the parts you added are not inverted, it was entirely 0 if I did not put the diagonal to 1 to the rows/columns I added. If I decided to put the diagonal, then the bytes you carefully injected are then reflected allong the dot product in this new bigger matrix. So either way you need to perform the same process to repatch everyting over this bigger matrix, infinetely recursing.
How it’s actually done
OK, so after this misadventure, the next step is to understand that a single element of coordinates (i, j) from the dot product is impacted by all elements of the ith line of the first matrix and all elements of the jth column of the second. (You actually already needed to understand this to implement my dumb idea but now we will make it interesting).
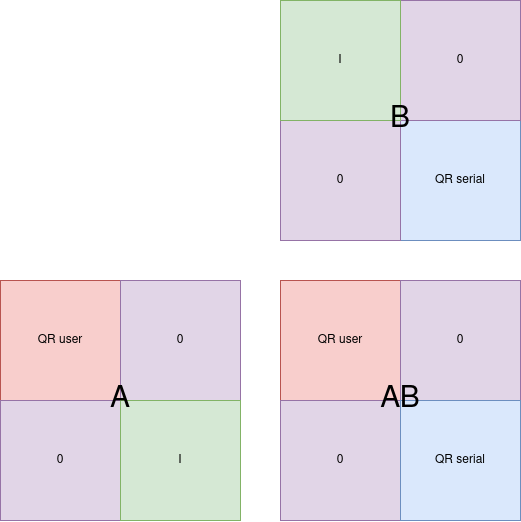
Let’s say that I take my first QR code and I double it’s height and width like this where the purple ones are all 0 matrices and the green one is the identity:

You can clearly see that if you patch any bytes in the identity matrix in the bottom right you will never impact the result of the top left corner of the dot product.
If you are not convinced: take this more striking example:
See how you can perform the dot product on each of the corner independently ? That is the key to solving this, because now instead of putting the identity matrix in the corresponding corner in the other image, we can simply compute the inverse of the QR code:
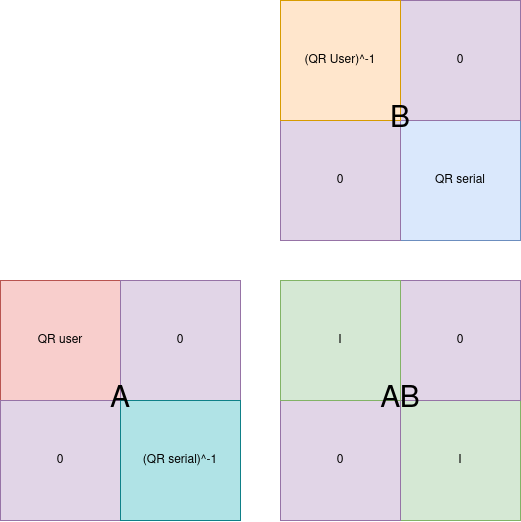
Inverting the two matrices
You may think “Ok this is over GG NO RE”, but it is not that simple, at least it wasn’t for me because I suck at maths.
So I tried multiple implementations of the matrix modular inversion, some worked, some didn’t, but most importantly, all of them took ages to run on actual images, about 10 minutes for most, and we are limited to 5 seconds on the remote service.
The best implementation was the sagemath one which computed real size images
inverses in about 20 seconds, still too slow. But at least I could test locally
that the generated images were accepted by the program, and they were, so I knew
I was on the right track.
I tried reducing the size of the QR code to make it faster, and it ran in less than a second, but the program could not recognize the data in the QR code anymore.
Well we need another strategy. First because it is taking too long, but also because not every matrix turns out to be invertible at all. And I don’t want to bruteforce the remote service to be lucky to have a username AND a serial matrix that are both invertible and then be lucky enough that the program successfully decodes the QR code.
If it isn’t invertible, juste make it invertible duh
So I go for a cleaner approach. I am not guaranteed that the QR code is invertible, fine, patch it to make it invertible.
And there is a really interesting property indeed:
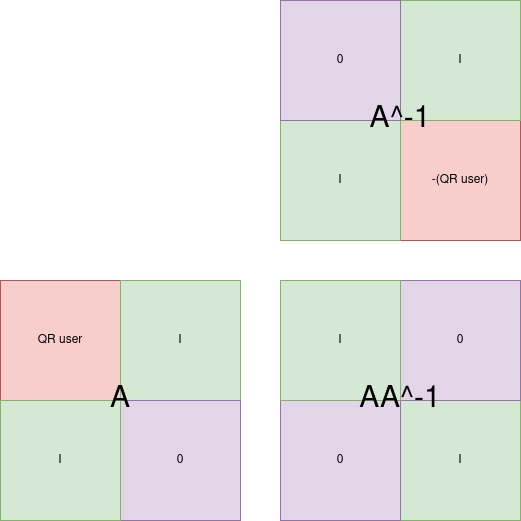
By adding identity matrices and an empty matrix in the bottom right corner, the
resulting matrix is always invertible, and the inverse can be trivially
computed since it is simply moving matrices arround and negating the original
image modulo 256 notice the "-(QRuser)" in the inverted matrix.
Putting everything together
So what we need to do given a random username:
- Compute its sha512 digest
- Compute the serial, the square of the matrix of the digest
- Generate a QR code for the digest and another one for the serial
- Make both QR code invertible by adding empty and identity matrices as shown above
- Compute the said inverse of said matrices
- In the result user.png put:
- The invertible digest QR code in the top left corner
- The inverted serial QR code in the bottom right corner
- In the result serial.png put:
- The inverted digest QR code in the top left corner
- The invertible serial QR code in the bottom right corner
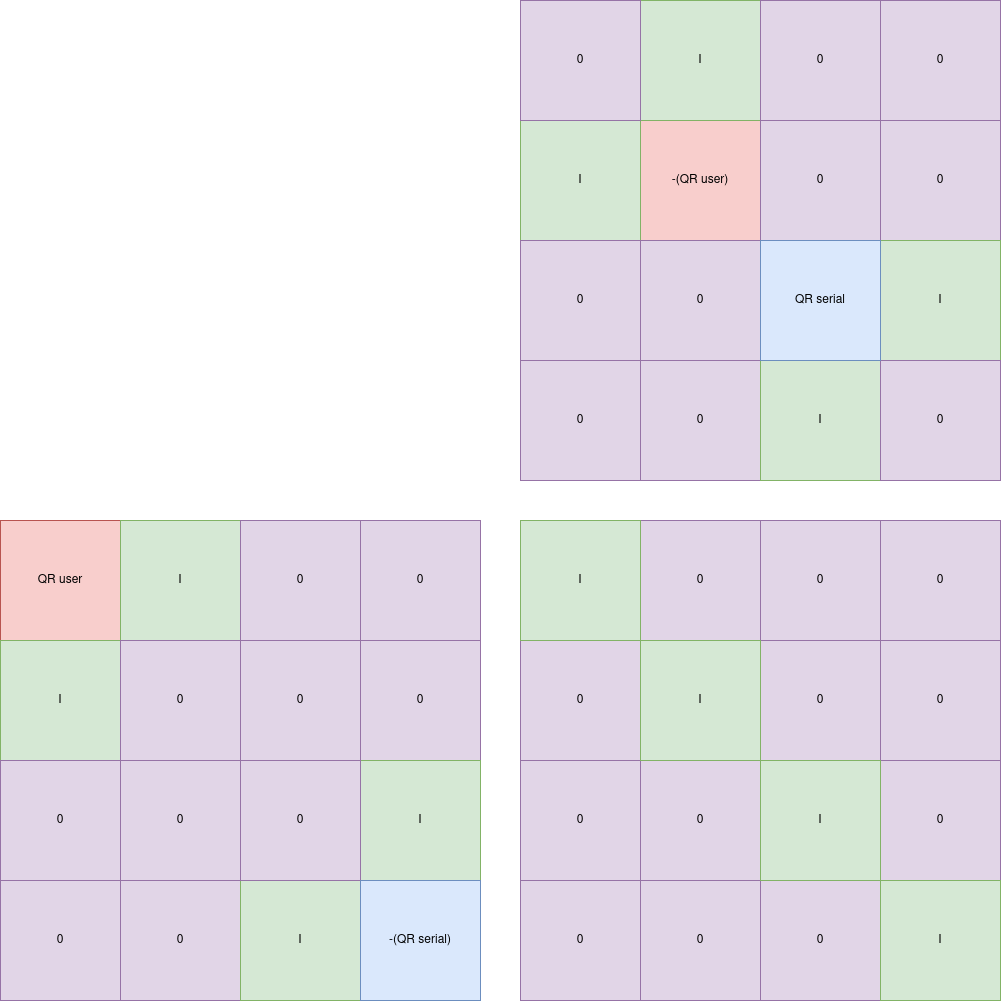
Solver
Here is the final solver script, which also automates fetching the username from the remote service and the upload of the images to recover the flag.
But before leaving this writeup there is still something I want to show you at the end.
#!/usr/bin/env python3
import hashlib
import qrcode
from PIL import Image
import numpy as np
import requests
def get_user():
r = requests.get("https://brachiosaure.france-cybersecurity-challenge.fr/")
name = r.text.split("text-warning\">")[1].split('<')[0]
return name
def get_digest(name):
m = hashlib.sha512()
m.update(name.encode())
digest = m.digest()
return digest
def linearize_serial(matrix_serial):
serial = bytearray()
for line in matrix_serial:
for b in line:
serial.append(b % 256)
return bytes(serial)
def img_to_matrix(img):
array = list(img.getdata())
width, height = img.size
matrix_img = [[array[i * width + j] for j in range(width)] for i in range(height)]
return matrix_img
def matrix_to_img(mat, path):
array = np.uint8(mat)
img = Image.fromarray(array)
img.save(path)
def gen_qrcode(data, path):
qr = qrcode.QRCode(version = 1, box_size = 2, border = 2)
qr.add_data(data)
qr.make()
qr_usr = qr.make_image()
qr_usr.save(path)
def identitymatrix(n):
return [[int(x == y) for x in range(0, n)] for y in range(0, n)]
def get_flag(name):
files = {
"upload1": open(f"{name}_usr.png", "rb"),
"upload2": open(f"{name}_serial.png", "rb")
}
r = requests.post("https://brachiosaure.france-cybersecurity-challenge.fr/login", files=files)
for line in r.text.split('\n'):
if "FCSC{" in line:
print(line)
name = get_user()
digest = get_digest(name)
matrix_usr = [[digest[i * 8 + j] for j in range(8)] for i in range(8)]
matrix_usr = np.array(matrix_usr)
matrix_serial = np.dot(matrix_usr, matrix_usr)
serial = linearize_serial(matrix_serial)
gen_qrcode(digest, "user.png")
gen_qrcode(serial, "serial.png")
img_usr = Image.open("./user.png", "r")
img_serial = Image.open("./serial.png", "r")
matrix_img_usr = img_to_matrix(img_usr)
matrix_img_serial = img_to_matrix(img_serial)
def invert(usr, serial):
# Add empty and identity matrices to make it invetible
usr = make_invertible(usr)
serial = make_invertible(serial)
n = len(usr)
# Total size after redimensionning
new_n = n * 2
# The magic inversion by swapping corners and computing matrix opposite
usr_inv = invert_magic(usr)
serial_inv = invert_magic(serial)
# Will hold the final user png
new_usr = []
# Will hold the final serial png
new_serial = []
# Create the new_usr
for i in range(new_n):
line = [0] * new_n
if i < n:
for j in range(n):
line[j] = usr[i][j]
if i >= n:
for j in range(n):
line[j + n] = int(serial_inv[i - n][j])
new_usr.append(line)
# Create the new_serial
for i in range(new_n):
line = [0] * new_n
if i < n:
for j in range(n):
line[j] = int(usr_inv[i][j])
if i >= n:
for j in range(n):
line[j + n] = serial[i - n][j]
new_serial.append(line)
return new_usr, new_serial
def make_invertible(mat):
res = []
n = len(mat)
ident = identitymatrix(n)
# Add the identity matrix below the original
for line in ident:
mat.append(line)
for i in range(len(mat)):
line = mat[i]
for j in range(n):
# Add the identity matrix at the right of the original
if i < n:
line.append(ident[i][j])
# Add the empty matrix at the bottom right corner
else:
line.append(0)
return mat
def invert_magic(mat):
n_tot = len(mat)
n = n_tot // 2
#Create a new empty matrix to hold the result
res = [[0 for _ in range(n)] for _ in range(n)]
ident = identitymatrix(n)
# Add the identity matrix below
for line in ident:
res.append(line)
for i in range(len(mat)):
line = res[i]
for j in range(n):
# Identity matrix on the right
if i < n:
line.append(ident[i][j])
# Oposite of the original in the bottom right corner
else:
el = -mat[i - n][j] % 256
line.append(el)
return res
res_usr, res_serial = invert(matrix_img_usr, matrix_img_serial)
matrix_to_img(res_usr, f"{name}_usr.png")
matrix_to_img(res_serial, f"{name}_serial.png")
get_flag(name)
$ ./solve_writeup.py
<strong>FCSC{c2ddbd0310bcf5f65c576453ee9697774afd38dc887b64f4dccc63ac598d084b}</strong>
Side notes
Here are examples of images generated by this solver for username 90QOCSdkzFE3rrYD2GdkrZkh4q:
The original user digest QR code:

The original serial QR code:

The patched user png

The patched serial png

As you can notice, there isn’t any noise visible by naked eye, this script therefore gets the flag 100% of the time.
Why is it so clean ? Simply because of the strategy we used to compute the inverse matrix:
-
We add empty matrices: they are black so no noise
-
We add identity matrices: they only have the diagonal set to 1 so only a little bit grayer than theso here you go.
-
We add the opposite of the matrix, and this is the clean part: our original matrices only hold black and white pixels so respectively
0x0and0xff, so the opposite of0is still0and the opposite of0xffif1modulo 256, so like the identity matrix, they are nearly invisible. If you look closely though 👀 you will see that all white pixels of the QR code were indeed reflected as very faint taint of gray in its inverse matrix on the other image.